|
NetKernel News Volume 2 Issue 9
December 17th 2010
What's new this week?
- Repository Updates
- ROC and Languages: Functions, Sets and ROC
- Book Review: Concepts of Modern Mathematics
Catch up on last week's news here
Repository Updates
The following package updates are available on both the NKEE and NKSE repositories...
- lang-javascript 1.3.1
- Added a workaround for a potential Rhino internal memory leak in E4X. Thanks to the Findlaw.com team for reporting and helping diagnose this.
- layer0 1.51.1
- Update to metadata and messages.properties
- module-standard 1.38.1
- Added warning reports of duplicate endpoint ID's in mapper configuration. Thanks to Carl Conradie for reporting this.
- nkse-dev-tools 1.28.1
- Fixed a duplicate endpoint id - which we found with the new warning!
ROC and Languages: Functions, Sets and ROC
In last week's fourth article I talked about the relationship between code and configuration. I demonstrated that to the ROC abstraction they are the same thing. I also showed how, when we think about sets of resources, we gain a useful perspective on functions.
Hopefully I gave a sense of ROC's innate language agnosticism. A valid solution provides the information we need irrespective of what the technical implementation is.
Turing Overkill
We also saw that there are compelling reasons to step back from Turing complete runtimes - not least in that a system composed out of configurable domain specific runtimes can be verifiably constrained and can have provable integrity.
For very many problems, starting off with the assumption that we must code in a Turing complete language is just overkill. You know the old adage: With great power comes great responsibility.
For systems coded with Turing complete languages you could rephrase it as:
With unlimited power comes unlimited responsibility.
Conversely for systems composed from extrinsically constrained configurable resource runtimes:
With constrained power comes limited liability.
Limiting Liability
The natural bias of an ROC system is towards limiting liability. The inherent risks and brittleness of full-fat code can be bounded and constrained and kept safely encapsulated within the black-box of Endpoints which, as the series has shown, are extrinsically composed with requests.
I'm not saying you never need to write low-level code. I'm just saying that in ROC it needn't be the default assumption and its certainly not the dominant task. (Made up number alert) Typically we see that classical code construction is at most 20% of an ROC solution's development work.
What I'm trying to convey is that ROC and its extrinsic model is an environment in which composition (structuring and mapping to extrinsic functions) and constraint (validation and introduction of boundary conditions) are what you spend most of your time doing.
*And* you gain the scope to introduce provability and quality assurance. *And* the economics of adapting to change are sane. *And*, as you're sick of hearing me say, it makes the system perform and scale better.
*And* you don't believe me...
Well fortunately just as I was writing this hysterical rant I got an email from Carl Conradie.
Carl works for a large insurance corporation and he's recently been self-teaching ROC/NK. His company has an existing portal and he decided to replicate it in NK. I gave him a small leg up by providing a simple bare-bones copy of the portal architecture we use for the NK services. This time last year it took me a day to knock that up (FYI its about a 100 lines of module spacial architecture - no "code", all composition of the pre-existing pieces that come with NK), so bare in mind that I gave him a day's head start.
With his permission, here's what he emailed me yesterday...
I just spent the most productive 48 hours of development in the last ten years.
The penny has dropped!!!!!!!!!!!!!!!!!!!!!!!!!!!!
I just duplicated using NK (and your portal) what a team of 6 developers accomplished in 3 weeks using RAD and WS portal.
Ok and it’s muuuuuuch faster.
I suspect you are conditioned to be extremely wary of blatant marketing hype like this. (If not, I know of a kind Nigerian prince who also corresponds with me and who I could put you in touch with).
However, if you followed last week's article, the fact that ROC allows you to think and work directly with sets of resources is the hard-core foundation to these practical values. As we've been building towards, and I hope to nail below, there is real substance behind my outrageous hype.
Today's Installment
For this week's sermon I'm going to push a bit further on our understanding of functions and from there try to offer a definition of ROC.
What is a Function?
The concept of a function is a strong contender for the most important in contemporary mathematics.
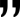
Ian Rose, Concepts of Modern Mathematics (see below)
Before you glaze over, this is not going to be a dry intricate examination of the mathematics behind functions (if that's what you expected look here).
Most of you, like me, will have had a technical education where at some point you were introduced to functions. You might have started with the linear function
y = m x + c
You almost certainly have a strong sense that in mathematics, functions are about the relationships between numbers - after all that's what maths courses spend most of their time concentrating on. Teaching you the tricks of the trade: adding, multiplication, division, drawing graphs, simultaneous equations, differential calculus etc etc.
As we learn computer languages we step away from mathematics to think about code and logic and variables, but still the basic sense of function we learnt in math(s) classes sticks with us. The functions we program take numerical values as their arguments, but we broaden it a bit and use String arguments and then broaden still further and have object references.
But ultimately, because we're programming on a Turing machine, all of these are still fundamentally relations between numbers (the state stored in the memory of the computer).
Some of you probably did some form of higher education maths course. This probably had some very dry formal definition of a function with terms like domain, range and target. (again look here for a recap). But, like me, you probably paid your dues, regurgitated the stuff in an exam and, if you thought about it at all, were satisfied that someone had bothered to put in place all this formal stuff but were pleased to move on.
I want to take you back to the foundations. I think we sometimes forget what we already know...
The Function Reloaded
Maths Symbol Reminder: When you see ∈ it means "element of". A membership relation between an object and a set. When you see ⊂ it means "is a subset of".
Right this is not going to be formal or complete, just a brief memory jogger and some pictures.
Firstly, the concept of a function is very general and also very simple. It can be stated in three lines. A function is:
- Domain D
- Target T
- A rule that for every x ∈ D specifies a unique element f(x) ∈ T
I said I'd keep it brief. What? That's not enough for you?
A function is a rule that takes a member of a first set (the Domain) to a member of a second set (the Target). "Rule" is a bit of a loaded term, so you can also say a mapping (from D to T). The critical part is that to be a function, the mapping must be unique: x maps to f(x) and nothing else.
It becomes a lot clearer with a picture...
Notice how general this is. We're not saying anything prescriptive about the nature of the sets or their elements. It could be the set of circles, the set of points on the Euclidean plain, the set of bitmap images.
The reason we have a preconception about functions is that most of our maths training spends its time concerned with techniques for manipulating functions where D and T are the set of real numbers ℝ.
Another interesting observation is that, the rule (mapping) doesn't have to be calculable. It just has to be valid in principal - it could be too expensive or just too hard to work out. Impracticality is not a limitation. We'll explore this a bit more later.
From the definition, represented in the previous diagram, it follows that there are some particular patterns which we can draw pictures of...
Surjection
When every element of T is mapped to by one (or more) elements of D the function is called a surjection.
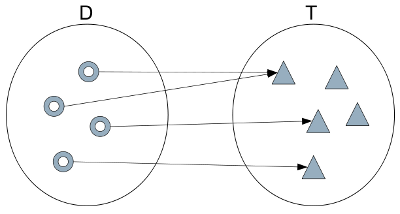
Injection
When every element of T is mapped to by at most one (but could be zero) elements of D the function is called an injection.
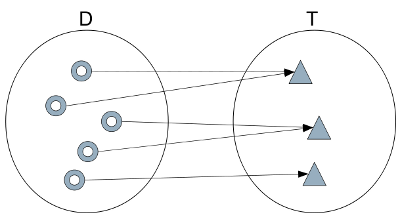
Bijection
When every element of T is mapped to by precisely one element of D the function is called a bijection.
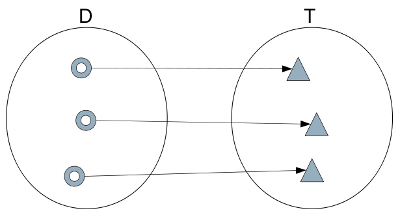
You can see that this is the combination of surjection and injection. If you turn the arrows round you still have a valid function from T to D, which is called the inverse function.
Bijections are the functions you'll be most familiar with. Take for example y = m x + c and the inverse x = ( y - c ) / m, given the x-coordinate of a point on the line you can uniquely determine y and vice versa.
Resources, Representations, Sets and Functions
Hopefully, you'll see that last week when I went off on my flight of fancy and started describing runtimes as bounded infinite sets I wasn't doing it for artistic effect. I was leading here and using the general set-based concept of a function.
Putting everything we've discussed together we can start to think about ROC using the core concepts of resources, representations, sets and functions.
What is the Web?
Let's warm up with a simple ROC system - a small subset of general ROC. Some people call it the "Web" and usually its described like this...
The World Wide Web, abbreviated as WWW and commonly known as the Web, is a system of interlinked hypertext documents accessed via the Internet. With a web browser, one can view web pages that may contain text, images, videos, and other multimedia and navigate between them via hyperlinks.
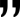
But I reckon we can do better if we step away from the trees...
The Web (W) is the set of all resources with identifier beginning "http". A Web Browser (B) is the set of all possible representations of resources. A Web page or Web application is a function which maps a subset A ⊂ W to B.
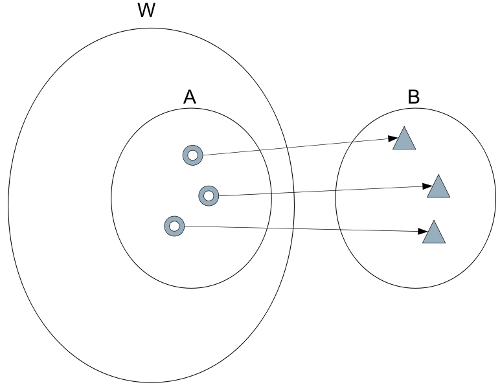
Now obviously, I am not being rigorous here. I'm assuming an instantaneous steady-state model where time is not a degree of freedom. I've also rolled-up the functions whereby B combines the representations into one composite rendered representation (the pixels in the view port) - these steps can be shown consistently, but they'd make it harder to get a sense of the big picture (and we'll need this picture when discussing ROC below).
I'm also omitting the "user function" which is a "function that selects functions" (aka navigates, adds input etc I don't want to open that can of worms). You also know that Javascript is now essential to web apps and you can think of it as time-domain (or user-driven) changes to the rendered representation but since we've frozen the time and user dimensions we can say javascript plays no part in the instantaneous state view.
However, hopefully with these caveats and without formal rigour, I think it offers a useful perspective.
For example, we can see that this example diagram is modelling a GET function. We can also visualize PUT and DELETE as functions from B to A. And we can see that POST is a mapping from B to A followed by a mapping from A' (A modified by received state) back to B.
We can see that W must contain the empty set - the resource we obtain when there is either no server hostname resolvable by DNS or the server does not have a web server.
We can also see the point and very raison-d'etre of the W3C has been to ensure that there is one global W that is consistent and well defined. And indeed, perhaps with lesser success, that there is one B (well at least a platonic B with many instances) every browser offers (approximately) the same set of all possible representations (see my article on HTML5 for a discussion on the approximate consistency of B instances). So the W3C, have ensured that the Web has matured such that it is a consistent function - given x we uniquely get f(x) no matter where we are in the internet.
As I confess, I'm not saying this is formally rigorous. But you can see that this treatment could be formalized. We can, in principal, consider the World Wide Web as the set of all Web-functions. Fortunately, the practicalities of computability don't exclude this - as discussed earlier.
Composite Applications
Is there a point to this? Am I just guilty of academic pontification? Hopefully not. I think this viewpoint gets to some deep truths. For example with it we can have a much better sense of architectural constructs like, for example, the mashup pattern...
We can represent the mashup pattern as follows:
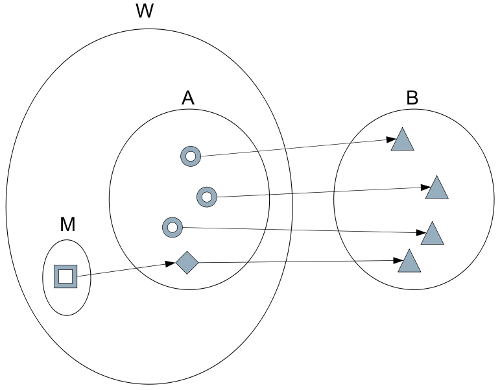
We can see that a mashup consists of an injection of set M into A and thence to B. Where A and M are subsets of W.
What is ROC?
As I have said many times before, ROC is a generalisation of the Web. But I've been guilty of not sweating the details to justify this crazy sounding claim (maybe its the physicist's psychosis "give me the general, spare me the details"). But maybe at this point we at last have a shared context with which I can attempt to justify my assertion...
ROC poses and answers the question: Why have just one W? Why not have as many W as we need at any scale and granularity. Why not create W on the fly. And, while we're at it, why not generalize B, to the set of all possible Turing computable state.
So ROC is a construct in which applications are functions mapping from an N-dimensional generalisation of W (which we have freedom to define) to the set B of all possible computable representations. (I confess I don't know how to draw a snappy diagram of this, however the new space explorer does give you some feel for it. However in the limit of a single space it collapses to the Web diagram shown above and with a self-consistency that doesn't require the caveats we gave for the Web discussion.)
ROC also introduces something new. A formal and consistent model for how we move from one W to another. In ROC the W are called spaces and the formal model is called resolution. We create applications A by defining function constructs that map from spaces to endpoints and so to representations (rep ∈ B).
You can now also see that the grammar is in fact a set description language. It enables the finite description of bounded infinite sets. (That's what we were doing last week when discussing the "interface" of active:imageRotate).
Furthermore, the mapper is a construct for logically defining functions (without the need for physical endpoint code). The mapper is general and permits us to define surjection, injection and bijection functions. (See why its called a mapper now? I've run out time but I was going to draw some diagrams of typical mappings and let you identify which type of function they implemented. I thought it would make a good game for your office party.)
With power over spaces and mappings we can implement simple composition patterns (internal "micro-mashups", spit!) but, unlike web mashups, we are not limited to injected subsets of a single space, we can construct elegant composite architectures of great sophistication and power spanning any number of spaces. (Ask Carl Conradie about the Portal structure if you think I'm losing it)
ROC allows us to step away from the minutiae of the "coding" and define broad extrinsic relations between sets. It follows that we can do more with less.
It also follows why ROC absorbs change. Change can be applied i) by introducing new sets with no side-effects on an existing solution and ii) by broadening existing sets whilst preserving legacy subsets. These factors alone shake the pillars of the economics of software.
We also gain a normalized view of all state in the system (we discover the members of B) and can consistently (due to the uniqueness critereon of functions) determine whether we actually really need to do any computing at all! (It runs faster - really!)
ROC is a generalisation of the Web. It may be a lot more besides, you tell me.
As I'll talk about next time, I don't think we've even started to scratch the surface of what it enables and what we'll discover...
Book Review: Concepts of Modern Mathematics, I. Stewart
I've been thinking directly or indirectly about the Web in terms of sets since we started back in HP over ten years ago. As we worked out ROC, and especially as we worked out the general ROC abstraction of NK 4 I had cause to go back and revisit many foundational pieces of Maths, Computer Science and Information Theory. You can't build on sand so we had to go and find some bedrock.
The informal treatment of functions I gave in the preamble above, owes a lot to chapter 5 of Ian Stewart's Concepts of Modern Mathematics.
Whether, like me, you've had quite a deep education in engineering maths. Or, you just did it in school and didn't have any exposure to formal maths in higher education. This is the book that I wished I'd known about earlier.
It succinctly covers all the key concepts in maths and, as I found, makes you realise why the heck some of the stuff was on the curriculum at all.
It claims, to be aimed at the general reader, but I think that's a bit optimistic. But its certainly very tractable for a reader with a technical background.
It would make a good stocking filler and give you something suitably intense and geeky to grumpily peer out from behind when the pressure of hanging with the in-laws gets too much.
Incidentally, there's a browsable selection on the Amazon site, and by luck there's the Appendix to chapter 5 in full at page 326 (slide down to it). Here he gives the more formal, pure set-theoretic, definition of function in terms of ordered pairs - that is, a function is itself a set. In many ways I think this is even more apposite for the Web and ROC but as he says its not as intuitive to start with this.
NetKernel West 2011: Call for Papers
The NetKernel West 2011 conference will take place 13-14th April 2011 in Fort Collins, Colorado, USA. The conference will be preceded by a one-day NetKernel bootcamp on the 12th where you can get a fast track immersion in NK and ROC before the main event.
We want to make this an open opportunity for the NetKernel ROC community. We invite you to please let us know if you would like a slot for a talk/presentation/demo etc.
| NetKernel West 2011 | |
| Location: | Fort Collins, Colorado, USA |
| Conference: | 13-14th April 2011 |
| NetKernel BootCamp: | 12th April 2011 |
We've now confirmed the conference venue and will be opening registration very soon.
Looking forward to meeting many of you face to face in April!
Have a great weekend.
Comments
Please feel free to comment on the NetKernel Forum
Follow on Twitter:
@pjr1060 for day-to-day NK/ROC updates
@netkernel for announcements
@tab1060 for the hard-core stuff
To subscribe for news and alerts
Join the NetKernel Portal to get news, announcements and extra features.
NetKernel will ROC your world
 |